Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
16(C4). Вписанный в окружность четырёхугольник с биссектрисами (вар. 43)
Комментарии к этой задаче: Комментарий добавил(а): Елена Спасибо, прекрасное решение. Комментарий добавил(а): Екатерина почему катеты KE и ET равны? Комментарий добавил(а): Лидия Ивановна такую задачу хорошо решать, когда есть свободное время, но только не на ЕГЭ! Издеваемся над учениками! Комментарий добавил(а): egetrener Лидия Ивановна, не согласна с Вами)) На таких замечательных задачах хорошо учиться. Это же тренировка мозгов, умения думать. Как ещё? Такого на ЕГЭ и не будет. Комментарий добавил(а): Галина Не пойму почему угол TAE равен углу TEA... Комментарий добавил(а): Галина Поняла, забыла, что AE - биссектриса Комментарий добавил(а): Флюра Спасибо Вам, Ольга! Не могли ли бы Вы решить С2? Хотя бы намеки какие-то. Комментарий добавил(а): Ольга Себедаш "почему катеты KE и ET равны?" Про это в задаче не сказано, они не равны. Комментарий добавил(а): Ирина не поняла, почему CD=KT Добавить Ваш комментарий: |
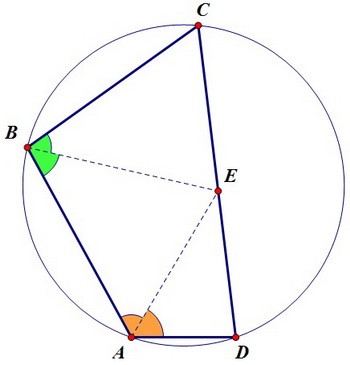Т.к. точка Е лежит на биссектрисе угла А, то она одинаково удалена от прямых АВ и АD.
Т.к. точка Е лежит на биссектрисе угла В, то она одинаково удалена от прямых АВ и ВС.
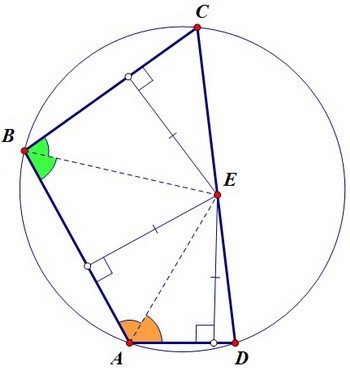Значит, точка Е одинаково удалена от прямых АD и ВС, что и требовалось доказать.
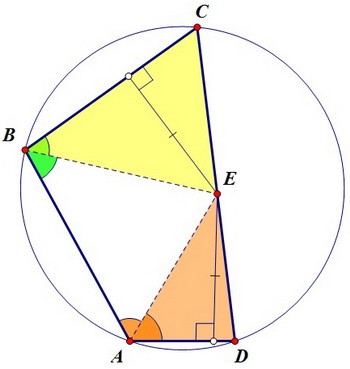Чтобы найти отношение площадей треугольников ADE и BCE с равными высотами,
надо найти отношения оснований, к которым эти высоты проведены, т.е. AD:BC.
Т.к. четырёхугольник вписан в окружность, то треугольники TCD и ТАВ подобны.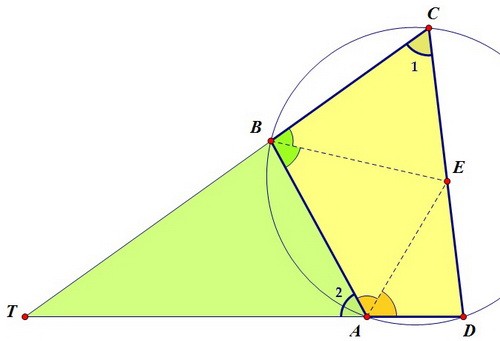
Это следует из того, что т.к. ∠1 + ∠BAD = 180° и ∠2 + ∠BAD = 180°, то ∠1 = ∠2.
Подобие красивое, но в данном случае нам понадобится именно равенство углов.
Через точку Е проведём отрезок КТ, параллельный стороне АВ. При этом ∠3 = ∠2.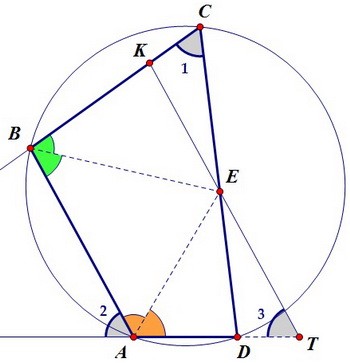
Образовавшиеся на рисунке треугольники КЕС и DЕТ равны. Докажем этот факт.
Для этого рассмотрим сначала голубые прямоугольные треугольники, они равны
по катету (доказано выше) и противолежащему острому углу. Поэтому ЕС = ЕТ.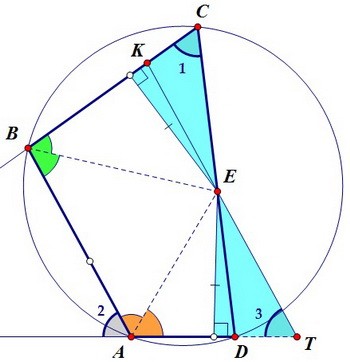
Красные треугольники КЕС и DЕТ равны по стороне и двум прилежащим к ней углам.
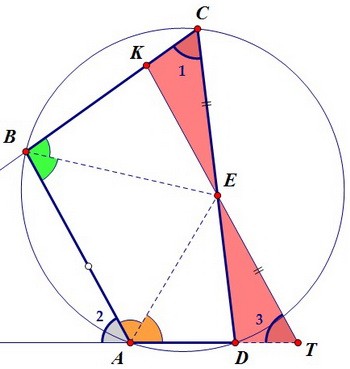Из равенства треугольников следует равенство сторон КЕ и DЕ, а также КС и DТ.
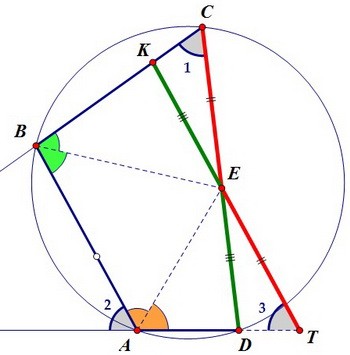Заодно замечаем, что сторона CD четырёхугольника равна длине отрезка КТ.
Из параллельности прямых КТ и АВ следует и равенство рыжих углов ТАЕ и ТЕА .
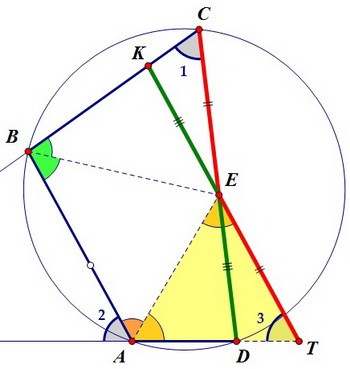Треугольник ТАЕ равнобедренный и ТА = ТЕ. Аналогично равны стороны КВ и КЕ.
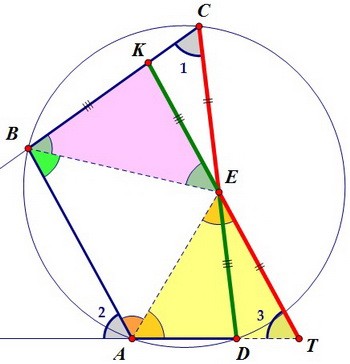Из полученных равенств делаем интересный вывод. Собираем по кусочкам сторону CD:
CD = KT = KE + TE = KB + AT = (BC - CK) + (AD + DT) = BC + AD + DТ - СК = BC + AD
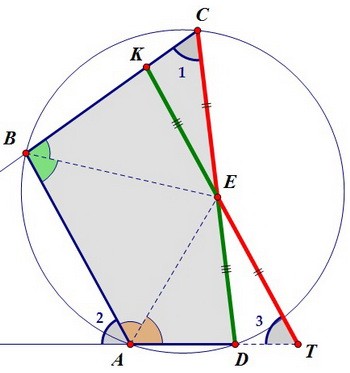Теперь учитывая данное отношение CD:BC = 3:2 и сделанный вывод CD = BC + AD,
получаем, что АD:BC = 1:2, и значит, SАDЕ:SBCЕ = 1:2.
Ответ: 1:2