|
Решите неравенство
}}\cdot{log_{x+3}{(3-x)}}\leq0)
Рассмотрим функцию
={log_{2-x}{(x+2)}}\cdot{log_{x+3}{(3-x)}}\leq0)
Основания логарифмов и подлогарифмические выражения должны быть больше нуля,
к тому же основания должны быть отличны от единицы. Находим область определения:
Таким образом, областью определения функции является интервал с выколотой точкой.=(-2; 1);(1; 2))
Вторым этапом найдём нули функции. Для этого приравняем нулю каждый множитель.
}=0) }=0)
Здесь важно помнить, что корни этих уравнений должны входить в область определения.
Только в этом случае их можно будет назвать нулями функции, и никак иначе!
Решим первое уравнение:
Из него следует, что х + 2 = 1, т.е. х = -1. Обратное, вообще говоря, неверно, т.е. х = -1
не является автоматически корнем логарифмического уравнения, требуется его проверка.
Точнее, требуется проверка, что при х = -1 основание логарифма больше 0 и не равно 1.
Рассмотрим второе уравнение:
Аналогично найдём и его корень: х = 2. Но он не входит в область определения функции.
Отсюда делаем вывод - функция обращается в ноль в единственной точке: х = -1.
На третьем этапе изобразим область определения и нули функции на оси ОХ.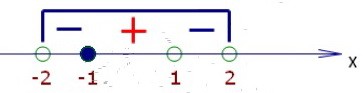 
И найдём знаки функции на интервалах, на которые -1 делит область определения.
Знаки определяем "в лоб", подставляя значение х из интервала в каждый множитель.
Проще всего подставить ноль из среднего интервала, оба множителя положительны.
Из правого промежутка подставим х = 1,5. Получим слева log0,5(3,5) · log4,5(1,5).
На языке логарифмов ноль записывается так: log0,5(1) или log4,5(1). Сравним:
log0,5(3,5) < log0,5(1) = 0 log4,5(1,5) > log4,5(1) = 0.
Мы учли при этом, что функция y = log0,5t убывает, а функция y = log4,5t возрастает.
В результате знак произведения log0,5(3,5) · log4,5(1,5) отрицателен на (1; 2).
Аналогично определяем знак функции на (-2; -1), взяв в качестве аргумента х = -1,5.
log3,5(0,5) < log3,5(1) = 0 log1,5(4,5) > log4,5(1) = 0.
В результате знак произведения log3,5(0,5) · log1,5(4,5) отрицателен на (-2; -1).
Ответ: (-2; -1]; (1; 2) Автор: Ольга Себедаш Просмотров: 5504
|
