Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Угол между стороной правильного n‐угольника, вписанного в окружность, и радиусом
этой окружности, проведенным в одну из вершин стороны, равен 80°. Найдите n.

Представим себе правильный многоугольник, вписанный в окружность.



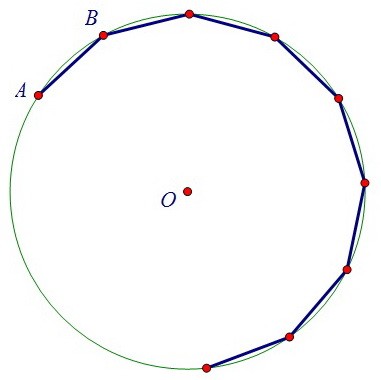Все стороны n-угольника равны и радиусы, проведённые к вершинам, разбивают
многоугольник ровно на n равных друг другу равнобедренных треугольников.



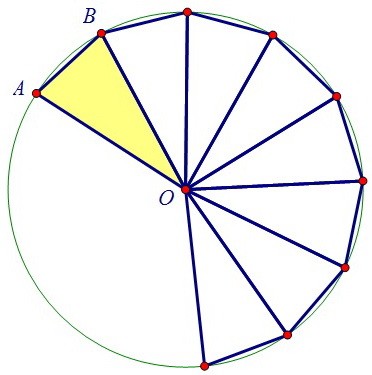В задаче дан угол при основании такого треугольника. Второй угол при основании равен ему.



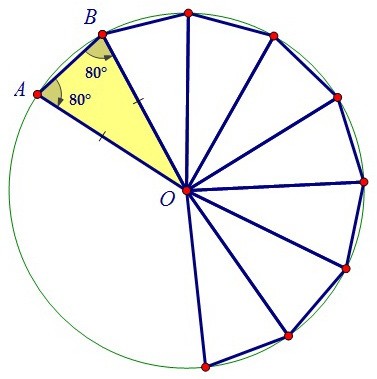Важно найти угол при вершине жёлтого треугольника и посчитать число треугольников.



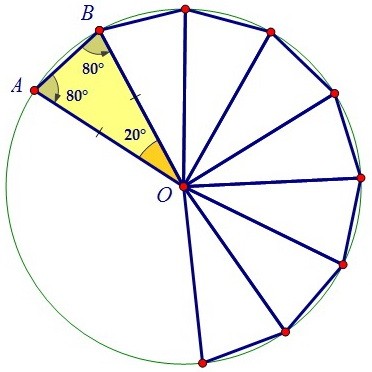∠АОВ = 180° - (80° + 80°) = 180° - 160° = 20°.

Угол при вершине О содержит 360°, а значит 18 раз по 20°.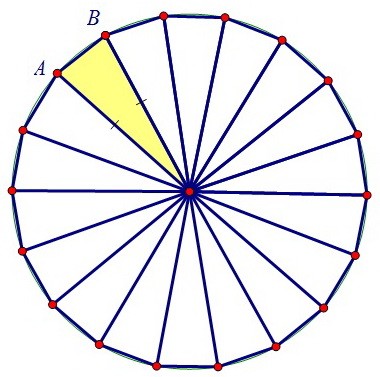



Многоугольник состоит из 18-ти равнобедренных треугольников,
а значит, из 18-ти сторон. Перед нами 18-тиугольник. n = 18.
Ответ: 18

Умышленно не использовала формулу суммы углов правильного многоугольника.

Автор: Ольга Себедаш             Просмотров: 29018