|
Найдите радиус окружности, вписанной в квадрат АВСD, считая стороны квадратных клеток равными √2.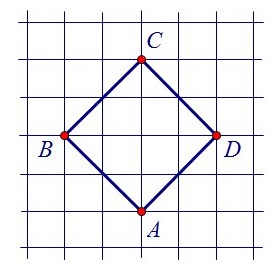
Центр окружности, вписанной в квадрат, лежит в точке пересечения его диагоналей.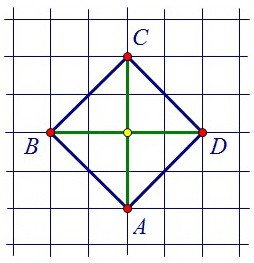
Радиус окружности перпендикулярен стороне квадрата. Треугольник ОВС равнобедренный,
и поэтому его высота ОТ является и медианой, точка Т - середина стороны ВС.
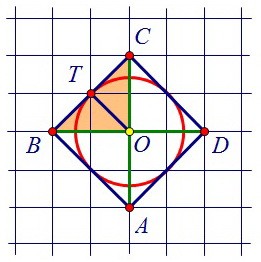Кроме того, радиус ОТ равен половине ТК, а ТК, в свою очередь, равен стороне квадрата.
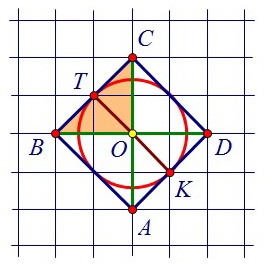Сторону квадрата можно найти из того же равнобедренного прямоугольного треугольника ОВС с катетом, равным по условию двум клеткам, т.е. 2√2.
Можно применить теорему Пифагора, а лучше помнить, что гипотенуза такого треугольника в √2 раз больше катета. ВС = ОВ · √2 = 2√2 · √2 = 2· 2 = 4.Ну а радиус окружности в два раза меньше стороны, т.е. равен двум.
Можно рассмотреть и прямоугольный равнобедренный треугольник ОВТ: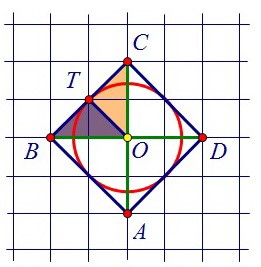
В нём известно, что гипотенуза ОВ равна 2√2, а найти требуется катет.
Из теоремы Пифагора следует, что катет в таком треугольнике в √2 раз меньше гипотенузы, т.е. равен двум.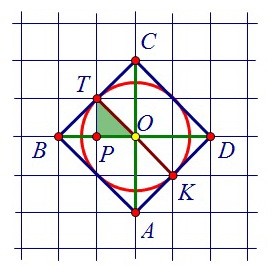
Наконец, можно рассмотреть крошечный прямоугольный треугольник РТО.
И он тоже является равнобедренным с катетом, равным по условию √2.
И его гипотенуза (искомый радиус) в √2 раз больше катета, т.е. равна 2.
Ответ: 2
Какой из трёх треугольников симпатичен именно Вам? Автор: Ольга Себедаш Просмотров: 35697
|
