|
В трапеции АВСD биссектриса угла А пересекает боковую сторону ВС в точке Е. Найдите площадь треугольника АВЕ, если площадь трапеции равна S, АВ = а, AD = b, CD = c, c меньше a.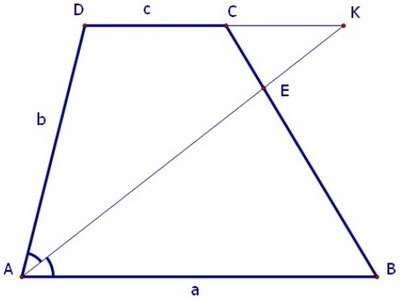
Заметим, что ∠2 = ∠3 как внутренние накрест лежащие при параллельных прямых и секущей.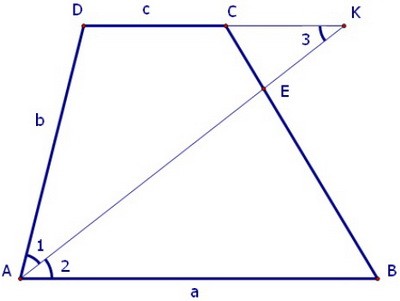 ∠1 = ∠2 по условию задачи. Значит, ∠1 = ∠3. И значит, треугольник ADK равнобедренный.
∠1 = ∠2 по условию задачи. Значит, ∠1 = ∠3. И значит, треугольник ADK равнобедренный.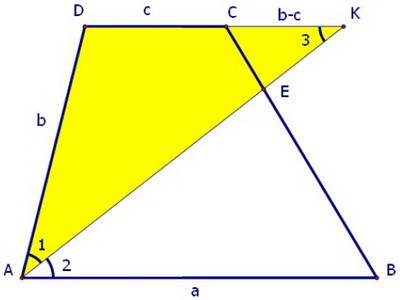 При этом DK = DA = b, поэтому СК = b - c. Треугольник СКЕ подобен треугольнику АВЕ.
К подобным треугольникам мы вернёмся, сначала рассмотрим треугольники СКЕ и СDE.
При этом DK = DA = b, поэтому СК = b - c. Треугольник СКЕ подобен треугольнику АВЕ.
К подобным треугольникам мы вернёмся, сначала рассмотрим треугольники СКЕ и СDE.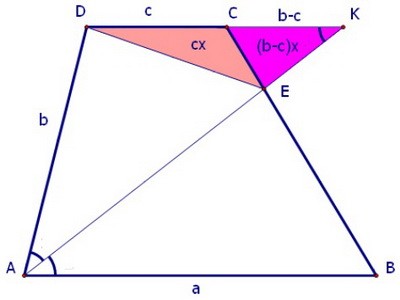 Площади этих треугольников относятся, как их основания CK и CD, т.к. высоты, проведённые к этим основаниям из точки Е, равны.
Обозначим площади треугольников (b - c)x и cx.
Площади этих треугольников относятся, как их основания CK и CD, т.к. высоты, проведённые к этим основаниям из точки Е, равны.
Обозначим площади треугольников (b - c)x и cx.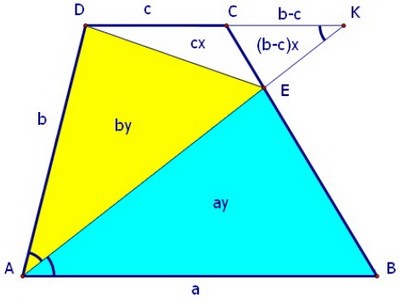 Теперь рассмотрим треугольники АВЕ и ADE. Их площади относятся, как а к b.Здесь мы учитываем, что у треугольников равные углы и общая сторона.
Теперь рассмотрим треугольники АВЕ и ADE. Их площади относятся, как а к b.Здесь мы учитываем, что у треугольников равные углы и общая сторона.
}}{2})
}}{2}) Обозначим площади этих треугольников аy и by.
Возвращаемся к подобным треугольникам СКЕ и АВЕ.
Обозначим площади этих треугольников аy и by.
Возвращаемся к подобным треугольникам СКЕ и АВЕ.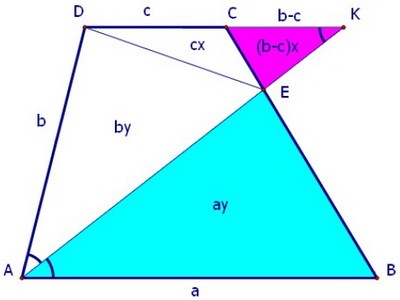 Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
x}{ay}=\frac{(b-c)^2}{a^2})
y) Теперь учтём, что по условию задачи площадь трапеции равна S.
Теперь учтём, что по условию задачи площадь трапеции равна S.
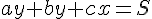 Мы получили два уравнения с двумя неизвестными x и y.
Выразим переменную x из первого уравнения.
Мы получили два уравнения с двумя неизвестными x и y.
Выразим переменную x из первого уравнения.
y}{a}) Подставим значение x во второе и выразим из него y.
Подставим значение x во второе и выразим из него y.
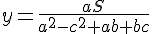 И наконец, учитывая, что SABE = ay, получим окончательно:
И наконец, учитывая, что SABE = ay, получим окончательно:
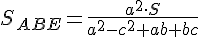 Автор: Ольга Себедаш Просмотров: 6229
|

