Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В пирамиде DABC известны длины рёбер AB = AC = DB = DC = 10, BC = DA = 12.
Найдите расстояние между прямыми DA и BC.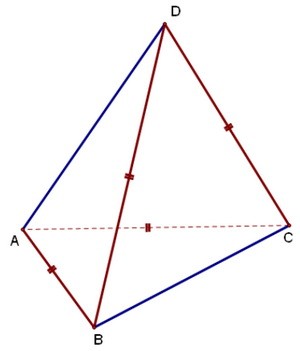

Равные рёбра на рисунке отмечены цветами. Цель - найти расстояние между синими рёбрами.
Обратим внимание на два равных друг другу равнобедренных треугольника: BDC и ВАС.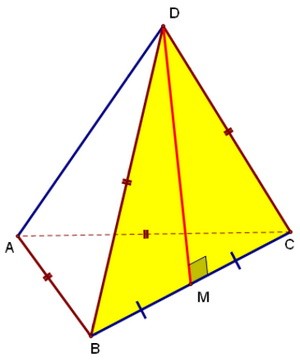



Напрашивается взять середину общего основания М и соединить её с вершинами D и А.
DМ в этом случае медиана, а значит, и высота треугольника ВDС, DМ ⊥ ВС.



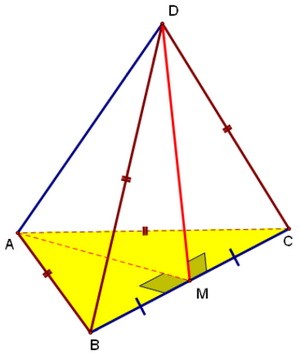Аналогично, АМ ⊥ ВС. Следовательно, ВС ⊥ АDМ по признаку перпендикулярности прямой
и плоскости (прямая ВС перпендикулярна двум пересекающимся прямым плоскости АDМ).



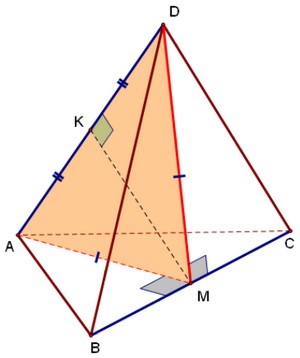Треугольник АМD равнобедренный, и его медиана МК, проведённая к АD, тоже является высотой.
Итак, МК ⊥ АD. Кроме того, МК ⊥ ВС по определению перпендикулярности прямой и плоскости
(т.к. ВС ⊥ АМD). Это значит, что МК и есть общий перпендикуляр к рёбрам DA и BC.
Найдём теперь длину отрезка МК, она и будет искомым расстоянием между прямыми.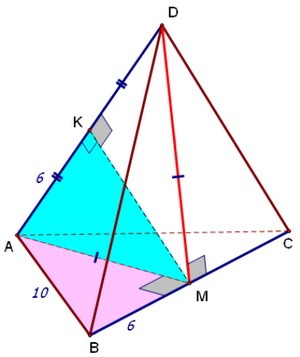



Из прямоугольного треугольника АВМ с гипотенузой 10 и катетом 6 находим, что АМ = 8.



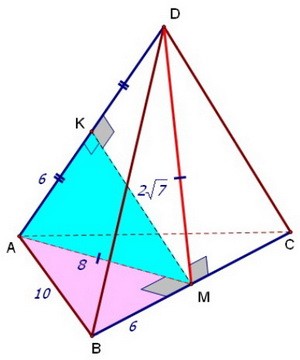А из прямоугольного треугольника АКМ с гипотенузой 8 и катетом 6 находим, что КМ = 2√7

Ответ: 2√7

Автор: Ольга Себедаш             Просмотров: 40837