Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Найдите все значения параметра а, при каждом из которых область значений функции



содержит отрезок [1; 2].

Для начала выразим косинус через синус и заменим параметр (a - 1) буковкой k.



Очевидна замена t = sinx. Очевидно также, что -1 ≤ t ≤ 1 в силу ограниченности синуса.
Перед нами стоит задача найти такие значения k, при которых найдутся значения t,
такие что функция сможет принять и значение 1, и значение 2.

                    

           

t² ≠ -k

Если бы функция при этом была бы непрерывна (в нашем случае знаменатель был бы отличен от нуля),
то этим дело бы и ограничилось. Непрерывная функция приняла бы все значения отрезка [1; 2].
На рисунках ниже примеры непрерывных функций, в область значений которых входит отрезок [1; 2].



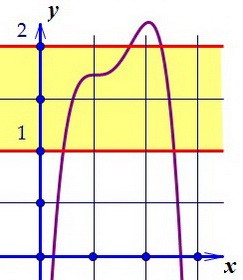
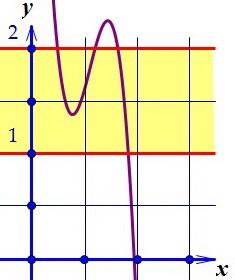
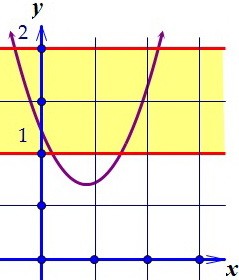Но нам придётся из найденных значений параметра выбросить те, при которых знаменатель обращается в ноль.
Причём, эти значения k нужно бы проверить, т.к. разрыв функции может произойти и вне нужного нам отрезка.

Разобьём задачу на три подзадачи:
1) Найдём значение параметра k, при которых уравнение t² - t + 3k = 0 имеет решения на [-1; 1].
2) Найдём значение параметра k, при которых уравнение 2t² - t + 4k = 0 имеет решения на [-1; 1].
3) Из найденных значений параметра исключим те, при которых t² = -k.

1) На оси t выделим отрезок [1; 1] и отметим первую координату вершины параболы 0,5.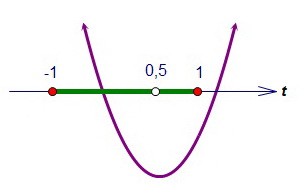



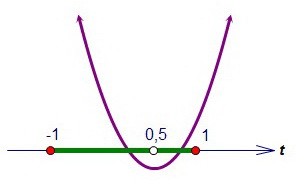Для существования корней квадратного трёхчлена вообще достаточно условия f(0,5) ≤ 0.
А для существования корней на [-1; 1] потребуем, чтобы f(-1) ≥ 0. Здесь учитываем симметричность
корней относительно точки 0,5 и тот факт, 1 ближе к 0,5, чем -1. При этом f(t) = t² - t + 3k.
В результате решения системы получим, что



2) Аналогично поступаем со второй задачей и получаем



Пересекаем получившиеся отрезки:



3) Вернёмся к первому уравнению t² - t + 3k = 0. Рассмотрим те значения параметра, при которых t² = -k.
Если t² = -k, то подставив это значение в уравнение, получим       -k - t + 3k = 0;      t = 2k;      t² = 4k²
Значит, 4k² = -k, т.е. мы получаем два значения параметра, при которых происходит разрыв: 0 и -0,25.
Проверив оба значения, исключаем только -0,25. В итоге для параметра k имеем

, 

Вернёмся к параметру а, прибавив к концам отрезка единицу:

,

Почему значение параметра, равное нулю, не выкидываем?

Автор: Ольга Себедаш             Просмотров: 22049