|
Через вершины А и В треугольника АВС проведена окружность, касающаяся прямой ВС, а через вершины В и С проведена ещё одна окружность, касающаяся прямой АВ.
Продолжение общей хорды BD этих окружностей пересекает отрезок АС в точке Е, а продолжение хорды AD одной окружности пересекает другую окружность в точке F.
а) доказать, что площади треугольников АВС и ABF равны;
б) найти отношение АЕ : ЕС, если АВ = 5 и ВС = 9.
Т.к. первая окружность проходит через точки А и В, её центр лежит на серединном перпендикуляре к АВ.
Т.к. она касается прямой ВС, то её центр лежит на перпендикуляре к ВС, проходящем через точку В.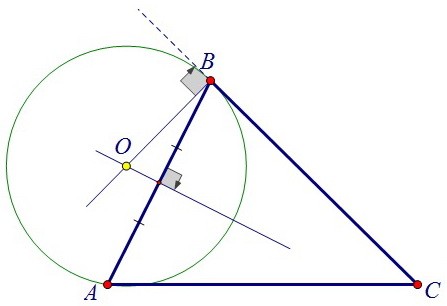 Аналогично рассуждаем при построении центра второй окружности.
Аналогично рассуждаем при построении центра второй окружности.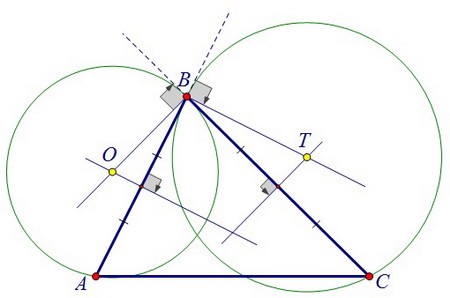 Продолжим хорду BD и отрезок AD так, как об этом сказано в условии.
Рассмотрим треугольники АВС и ABF.
Продолжим хорду BD и отрезок AD так, как об этом сказано в условии.
Рассмотрим треугольники АВС и ABF.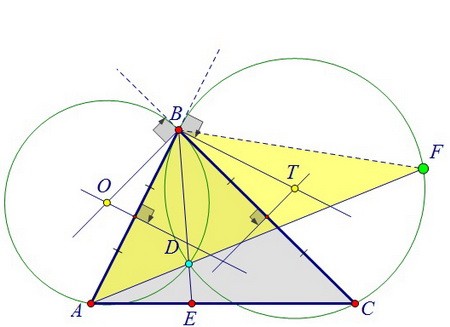 Чтобы доказать равенство площадей треугольников с общим основанием АВ,
достаточно доказать равенство их высот, проведённых из вершин С и F.
Здесь для равенства высот необходима параллельность прямых АВ и СF.
А для параллельности прямых необходимо равенство углов ВАF и AFC.
Чтобы доказать равенство площадей треугольников с общим основанием АВ,
достаточно доказать равенство их высот, проведённых из вершин С и F.
Здесь для равенства высот необходима параллельность прямых АВ и СF.
А для параллельности прямых необходимо равенство углов ВАF и AFC.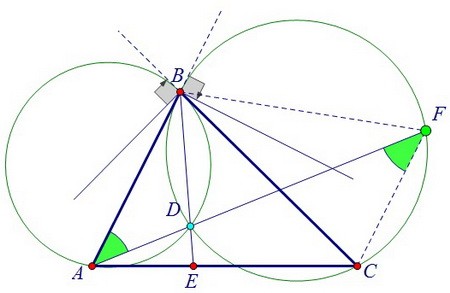 Чтобы показать равенство зелёных углов 1 и 2, рассмотрим третий угол DВС.
Чтобы показать равенство зелёных углов 1 и 2, рассмотрим третий угол DВС.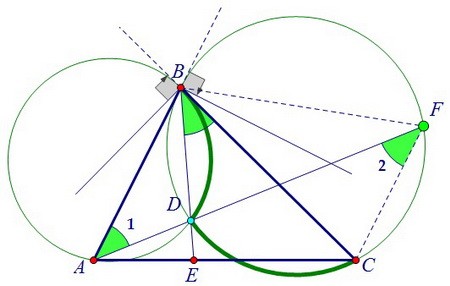 ∠DВС = ∠DFC, т.к. оба угла вписаны во вторую окружность и опираются на одну и ту же дугу DC.
С другой стороны, ∠DВС - это угол между хордой и касательной, проходящей через конец хорды
Следовательно, угол DВС равен половине дуги BD. Но и вписанный в первую окружность угол BAD тоже равен половине дуги BD. Таким образом, ∠DBC = ∠BAD. И значит, ∠DFC = ∠BAD.
Итак, мы доказали равенство углов ВАF и AFC. Из равенства углов вытекает параллельность прямых АВ и СF.Из параллельности прямых следует равенство высот треугольников АВС и ABF.А из равенства высот, проведённых к общему основанию, следует равенство площадей треугольников.
Приступаем к пункту б) и найдём отношение АЕ : ЕС, если АВ = 5 и ВС = 9.
Заметим, что равенство рыжих углов на рисунке аналогично равенству зелёных.
∠DВС = ∠DFC, т.к. оба угла вписаны во вторую окружность и опираются на одну и ту же дугу DC.
С другой стороны, ∠DВС - это угол между хордой и касательной, проходящей через конец хорды
Следовательно, угол DВС равен половине дуги BD. Но и вписанный в первую окружность угол BAD тоже равен половине дуги BD. Таким образом, ∠DBC = ∠BAD. И значит, ∠DFC = ∠BAD.
Итак, мы доказали равенство углов ВАF и AFC. Из равенства углов вытекает параллельность прямых АВ и СF.Из параллельности прямых следует равенство высот треугольников АВС и ABF.А из равенства высот, проведённых к общему основанию, следует равенство площадей треугольников.
Приступаем к пункту б) и найдём отношение АЕ : ЕС, если АВ = 5 и ВС = 9.
Заметим, что равенство рыжих углов на рисунке аналогично равенству зелёных.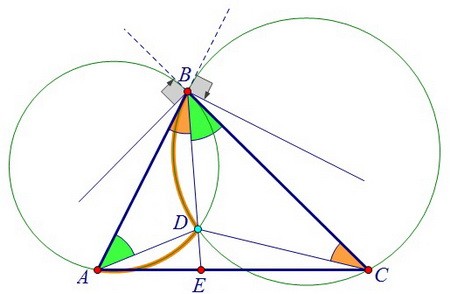 Треугольники ABD и CBD оказываются подобными. И значит, ∠ADB = ∠BDC. Ну и отсюда ∠ADE = ∠CDE. Треугольники ABD и CBD оказываются подобными. И значит, ∠ADB = ∠BDC. Ну и отсюда ∠ADE = ∠CDE.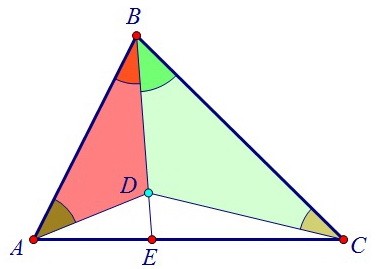 Получается, что в треугольнике ADC отрезок DE является биссектрисой. И мы близки к решению.
Получается, что в треугольнике ADC отрезок DE является биссектрисой. И мы близки к решению.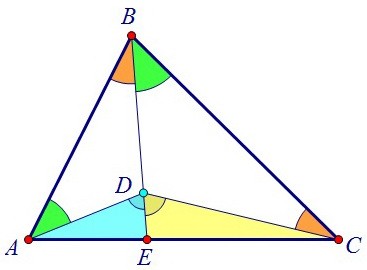 По свойству биссектрисы треугольника АЕ : ЕС = DA : DС. Второе отношение ищем из подобия треугольников ABD и CBD.
По свойству биссектрисы треугольника АЕ : ЕС = DA : DС. Второе отношение ищем из подобия треугольников ABD и CBD.
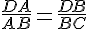
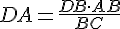
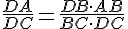
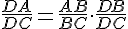
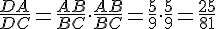 Ответ: АЕ : ЕС = 25 : 81
Ответ: АЕ : ЕС = 25 : 81 Автор: Ольга Себедаш Просмотров: 16265
|

 Аналогично рассуждаем при построении центра второй окружности.
Аналогично рассуждаем при построении центра второй окружности. Продолжим хорду BD и отрезок AD так, как об этом сказано в условии.
Рассмотрим треугольники АВС и ABF.
Продолжим хорду BD и отрезок AD так, как об этом сказано в условии.
Рассмотрим треугольники АВС и ABF. Чтобы доказать равенство площадей треугольников с общим основанием АВ,
достаточно доказать равенство их высот, проведённых из вершин С и F.
Здесь для равенства высот необходима параллельность прямых АВ и СF.
А для параллельности прямых необходимо равенство углов ВАF и AFC.
Чтобы доказать равенство площадей треугольников с общим основанием АВ,
достаточно доказать равенство их высот, проведённых из вершин С и F.
Здесь для равенства высот необходима параллельность прямых АВ и СF.
А для параллельности прямых необходимо равенство углов ВАF и AFC. Чтобы показать равенство зелёных углов 1 и 2, рассмотрим третий угол DВС.
Чтобы показать равенство зелёных углов 1 и 2, рассмотрим третий угол DВС. ∠DВС = ∠DFC, т.к. оба угла вписаны во вторую окружность и опираются на одну и ту же дугу DC.
С другой стороны, ∠DВС - это угол между хордой и касательной, проходящей через конец хорды
Следовательно, угол DВС равен половине дуги BD. Но и вписанный в первую окружность угол BAD тоже равен половине дуги BD. Таким образом, ∠DBC = ∠BAD. И значит, ∠DFC = ∠BAD.
Итак, мы доказали равенство углов ВАF и AFC. Из равенства углов вытекает параллельность прямых АВ и СF.Из параллельности прямых следует равенство высот треугольников АВС и ABF.А из равенства высот, проведённых к общему основанию, следует равенство площадей треугольников.
Приступаем к пункту б) и найдём отношение АЕ : ЕС, если АВ = 5 и ВС = 9.
Заметим, что равенство рыжих углов на рисунке аналогично равенству зелёных.
∠DВС = ∠DFC, т.к. оба угла вписаны во вторую окружность и опираются на одну и ту же дугу DC.
С другой стороны, ∠DВС - это угол между хордой и касательной, проходящей через конец хорды
Следовательно, угол DВС равен половине дуги BD. Но и вписанный в первую окружность угол BAD тоже равен половине дуги BD. Таким образом, ∠DBC = ∠BAD. И значит, ∠DFC = ∠BAD.
Итак, мы доказали равенство углов ВАF и AFC. Из равенства углов вытекает параллельность прямых АВ и СF.Из параллельности прямых следует равенство высот треугольников АВС и ABF.А из равенства высот, проведённых к общему основанию, следует равенство площадей треугольников.
Приступаем к пункту б) и найдём отношение АЕ : ЕС, если АВ = 5 и ВС = 9.
Заметим, что равенство рыжих углов на рисунке аналогично равенству зелёных. Треугольники ABD и CBD оказываются подобными. И значит, ∠ADB = ∠BDC. Ну и отсюда ∠ADE = ∠CDE.
Треугольники ABD и CBD оказываются подобными. И значит, ∠ADB = ∠BDC. Ну и отсюда ∠ADE = ∠CDE. Получается, что в треугольнике ADC отрезок DE является биссектрисой. И мы близки к решению.
Получается, что в треугольнике ADC отрезок DE является биссектрисой. И мы близки к решению. По свойству биссектрисы треугольника АЕ : ЕС = DA : DС. Второе отношение ищем из подобия треугольников ABD и CBD.
По свойству биссектрисы треугольника АЕ : ЕС = DA : DС. Второе отношение ищем из подобия треугольников ABD и CBD.