Егэ-тренер. Подготовка 2017-2018 Тренинги в прямом эфире для учителей и учеников |
|
4. Злоключения паука. Выбор верного пути и вероятность победы (вар. 41)
Комментарии к этой задаче: Комментарий добавил(а): Валя И как это я сама не догадалась? Комментарий добавил(а): Надя Глубокая благодарность!!! Комментарий добавил(а): Александр Хорошая и полезная задача Комментарий добавил(а): Зина а почему вероятность равна 0,5? Комментарий добавил(а): egetrener Потому что всегда есть два пути. Комментарий добавил(а): Эпловский вероятность точно так считается? , я думал там все пути искать у меня 1/8 получилось вначале а тут другой ответ Комментарий добавил(а): Лама увлекательные приключения с пауком Комментарий добавил(а): Степан Проблема паука терзала мой мозг длительное время. Спасибо, что разъяснили. Комментарий добавил(а): Саня а почему нужно умножать? я думал нужно складывать. Комментарий добавил(а): Ольга Себедаш Саня, при сложении вероятность увеличится. Не находишь это странным? Комментарий добавил(а): марина я не смогла ее решить Комментарий добавил(а): Марина а оказывается она такая легкая я уже разобралась Комментарий добавил(а): Алина Большое спасибо.:-) Комментарий добавил(а): Валера вам не кажется , что вероятность слишком мала, МЕНЬШЕ ОДНОГО ПРОЦЕНТА Добавить Ваш комментарий: |
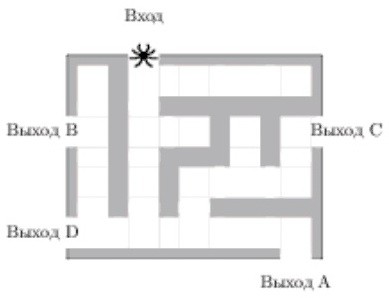Развернуться и ползти назад паук не может. На каждом разветвлении
паук выбирает путь, по которому ещё не полз.
Считая выбор дальнейшего пути случайным, определите,
с какой вероятностью паук придёт к выходу А.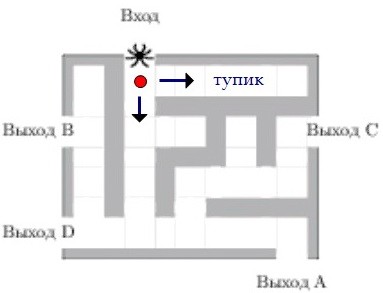
Вероятность пойти правильным путём (а не в тупик) равна 0,5.
Попав в жёлтую точку, он задумывается второй раз.
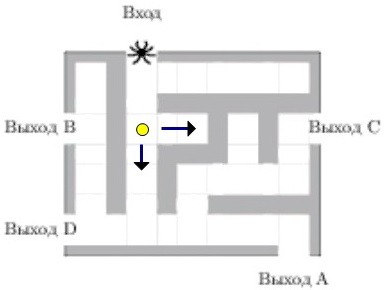Вероятность не сбиться с маршрута опять умножается на 0,5.
Но и это ещё не всё! В голубой точке перед пауком вновь выбор.
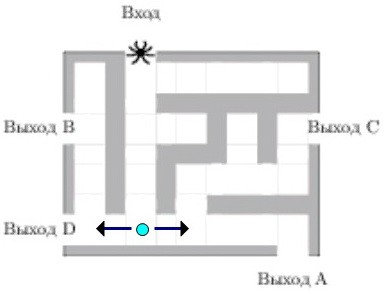И опять вероятность достичь цели уменьшается в два раза.
Последнее испытание ждёт паука в зелёной точке.
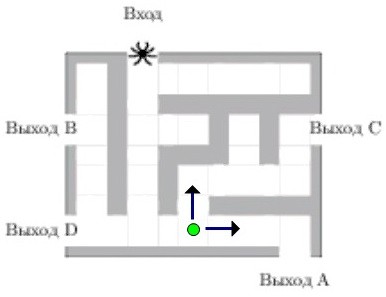Вероятность напоследок снова умножается на 0,5.
Что же мы с пауком имеем в итоге? А имеем мы вот что:
0,5 · 0,5 · 0,5 · 0, 5 = 0,0625
Ответ: 0,0625
