|
Найдите все значения а, для которых при каждом х из промежутка (3, 9]
значение выражения log32x + 3log3x не равно значению выражения 9 + аlog3х.
Сделаем замену t = log3x и заметим, что 1 < t ≤ 2 (из условия).
Перенесём все слагаемые влево и рассмотрим квадратичную функцию
f(t) = t2 + (3-a)t - 9. Т. к. D>0 (найдите его), то трёхчлен имеет два корня.
Найдём все а, при кот. на (1 , 2] парабола не пересекает ось OX.
При этом возможны три случая (рассмотрим их по порядку):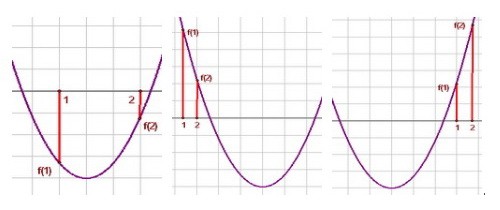
Предварительно найдём:
f(1)=1+(3-a)-9=-a-5; f(2)=4+2(3-a)-9=-2a+1; Xвер=0,5a-1,5.
1) Достат. потребовать выполнение условий f(1) ≤ 0 и f(2) < 0.
2) Кроме условий f(1) > 0 и f(2) > 0, требуем: Xвершины > 2.
3) Кроме условий f(1) ≥ 0 и f(2) > 0, требуем: Xвершины < 1.
Результат решения пункта 1): a > 0,5,
результат решения пункта 2): пустое множество,
результат решения пункта 3): a ≤ -5.
В ответе объединяем полученное: (-∞ , -5], (0,5 , +∞)
Ответ: (-∞ , -5], (0,5 , +∞)
Автор: Ольга Себедаш Просмотров: 20626
|
